Table of contents
This is a brief summary of all the important concepts of ECE 109 Materials Chemistry @UWaterloo. (With a few deep dives.)
First, the course description:
This course will help students understand the relationship between the microstructure of common semiconductor and optoelectronic materials, and the electrical, optical, and magnetic properties exhibited by the materials. Topics include structure of atoms, models of the atom, electronic configuration, band theory, atomic bonding, dielectric properties, optical transparency, magnetic properties, molecular bonding, metals and alloys, and activation energy. [Offered: F,W]
The main course material is in one standard text, Introduction to Materials Science for Engineers by James F. Shackelford.
The most important takeways:
- Structure leads to properties
We explain the behaviour of the materials used in engineering designs by looking at their internal structures
- Atomic bonding is the key determiner of material classification
Metallic bonding gives metals their strength, ionic bonding gives ceramics and glasses their stability, and covalent bonding gives polymers their formability.
- Stability corresponds to an energy minimum
To change a system, energy must be supplied
Materials
There are six categories of engineering materials:
- Metals
- metallic bonding, high ductility, high lustre, good conductor, crystalline
- Ceramics
- Ionic bonding (oxides), chemically stable, temperature-resistant (refractory), brittle
- Chemically composed of one metallic element and one of C, N, O, P, S
- Can be made noncrystalline
- silicates
- Glasses (see Ceramics, but with additional optical properties)
- Polymers (or plastics)
- Covalent bonding, Formability, ductility, lightweight, lower melting point, higher chemical reactivity
- Composites
- Best properties of each material type incorporated producing a superior product than either individual material
- Semiconductors
- Small group of elements and compounds that are neither good conductors nor insulators
- Si, Ge, Sn serving as bounhdary between metallic and non-metallic elements.
- precise control of chemical purity allows precise control of electronic properties
- show similarities to ceramics/glasses
The first four categories are associated with three distinct types of atomic bondings.
What are atoms?
All matter is made up of atoms. Atoms are made up of protons, neutrons, and electrons.
- Protons have a positive charge of $e$ (elementary charge)
- Neutrons have no charge
- Electrons have negative charge of $-e$
Where $e \approx 1.6\times 10^{-17}\text{C}$.
Elementary particles of the same type are all the same. That is, two protons always have the exact same properties.
In the planetary model sufficient for materials science, we make the following assumptions:
- The protons and neutrons form the fixed centre of the atom.
- Electrons orbit the atom in certain regions called "orbitals."
- Electrons have negligible mass.
- The majority of the atom's volume is empty.
This immediately leads to a few conclusions:
- The mass of an atom is equal to the sum of the masses of protons and neutrons.
- Protons and neutrons both have a mass of $\approx 1.66\times 10^{-24}\text{g}$
- The "type" of an atom must be determined by the number of protons, which change both the inherent positive charge and weight of the atom.
- The chemical bonding properties of atoms must be determined by the electrons, since they both hold charge and move.
Elements and isotopes
Every atom with a different number of protons is called an "element." These are listed on the periodic table. Each element has a name and corresponding letters to identify it. The atomic number of an element is the number of protons it contains.
An example of an element is carbon. All carbon atoms must have six protons.
Isotopes are different varietes of the same element. Since elements are purely defined by the number of protons they have, the isotopes of an element are the different number of neutrons they may possess. Isotopes are named after the total number of protons and neutrons they have. For example, carbon-12 is an isotope of carbon with 12 - 6 neutrons.
Elements are indicated using the notation:
$$^\text{A}_\text{Z} \text{X}$$
- $\text{X}$: atomic symbol of the element
- $\text{A}$: atomic mass
- $\text{Z}$: atomic number
Elements in the periodic table are grouped. Elements in the same column have similar chemical properties.
Atomic bonding
Atomic bonding provides a classification scheme for materials.
Metallic, ionic, and covalent bonding roughly correspond to the categories of structural materials: metals, ceramics/glasses, and polymers.
There are two types of bonds: primary bonding and secondary bonding.
- Primary bonding: transfer or sharing of electrons creating a strong bond, as in ionic, covalent, and metallic bonds
- Secondary bonding: weaker bonding that nevertheless influence material properties, like that from the Van der Waals force.
Atomic bonding involves electrons and electron orbitals. An atom with more electrons will have more orbitals. Each orbital of electrons has a corresponding energy level, a fixed energy between the electron and its nucleus.
The bonding of atoms is an electronic process. Primary bonds form where outer orbital electrons are transferred or shared between atoms. Secondary bonds result from a subtle attraction between positive and negative charges with no actual electron sharing/transfer.
Fundamentally, all forms of bonding occur because atoms want to have a filled outer shell of electrons in a stable configuration.
Analysis of bonding
The bonding energy $E$ is related to bonding force:
$$F = \frac{dE}{da}$$
Ionic bond
Ionic bonds occur when an atom transfers some electrons to another atom to form cations and anions.
- Ions are charged atoms.
- Cations are postively charged atoms.
- Anions are negatively charged atoms.
The atom that "gives away" its electrons will have a stable outer shell and become a cation. Likewise, the atom that receives electrons will also have a stable outer shell and become an anion.
Afterwards, the cation and anion are electrostatically attracted to each other. This attraction forms a strong bond.
The ionic bond is:
- Nondirectional: cations will be attracted to bonded anions equally in all directions
- Often ions "stack together" systematically to maximize the number of oppositely charged ions adjacent to any given ion.
- Coulombic: the attraction between ions is due to the coulombic force, which increases dramatically as the separation distance $a$ decreases.
$$F_c = \frac{-K}{a^2}$$
Bond lengths are not zero because the coulombic attraction is counteracted by an opposing exponential repulsive force due to the overlapping similarly charged electric fields of each ion.
$$F_r = \lambda \exp{\left (-\frac{a}{r}\right )}$$
Bonding force referso the net attraction or repulsion as a function of separation distance between two atoms or ions. The equilibrium bond length $a_0$ occurs where the forces of attraction and repulsion are precisely balanced;
$$F_c + F_R = 0$$
For ionic bonds, this is the sume of the two ionci radii and implies that the two ions are hard spheres touching at a single point.
The coordination number of an ion is the number of adjacent ions (or atoms) surrounding a reference ion. The coordination number of the smaller ion depends directly on the relative sizes of the oppositely charged ions. This relative size is characterized by the radius ratio (r/R) where $r$ is the radius of the smaller ion and $R$ is the radius of the larger one.
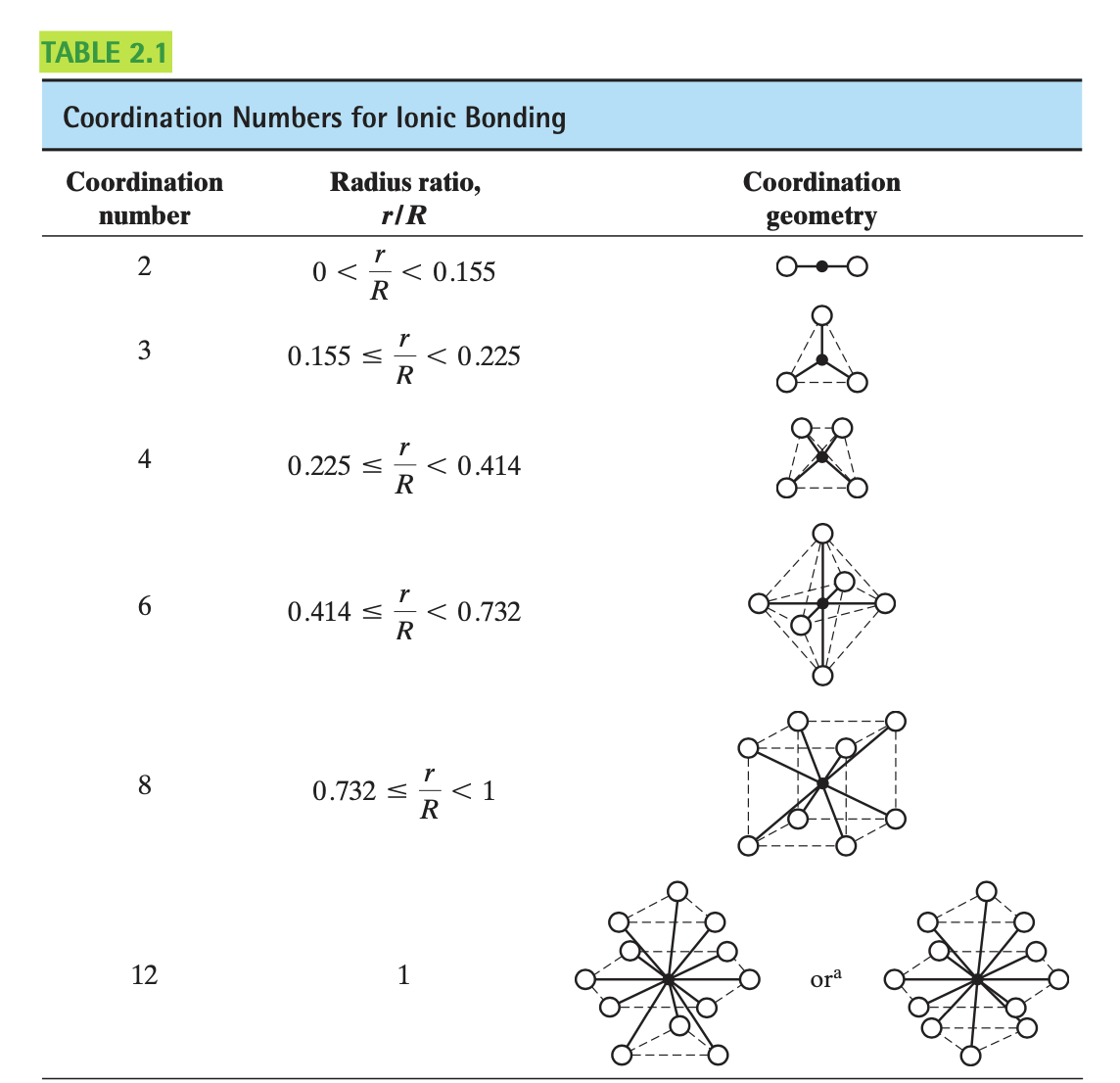
The percentage ionic character of a bond can be approximated as:
$$IC = 1 - e^{(-\frac{1}{4}(X_A - X_B)^2)}$$
$$\%IC = 100 * IC$$
Materials selection
Crystal structures
Dense orderly packed crystal structures tend to have lower energies or to be more stable. The distances between neighbouring atoms in a single crystal must be the same and equal to the bond length, $\bar{a} = a_0$
The average distances between neighbouring atoms in a polycrystalline or amorphous material is greater than the bond length, $\bar{a} > a_0$
The packing pattern of the atoms or ions forming a crystal depends to a large degree on their coordination number.
Definition 1: Coordination number (crystal)
The number of ions immediately surrounding an ion of the opposite charge within a crystal lattice.
Unit cell
The unit cell defines the simplest structural unit of a crystal at the atomic level. This means that the crystal can be formed from the repeated translation of the cell.
Definition 2: Unit cell
The simplest structural unit of a crystal. Note: "unit" does not refer to any physical properties like volume or mass.
Defined by the lengths of its three axes $a, b, c$ and the angles $\alpha, \beta, \gamma$ around the same corner.
In this way unit cells are specified like parallelpipeds.
Lattice points
Volumeless lattice points are used to describe the arrangements of atoms or ions in a crystal structure. One lattice point can be associated with more than one atom or ion.
The seven crystal systems
The seven crystal systems are
| System | Lengths | Angles |
|---|---|---|
| Cubic | $a = b = c$ | $\alpha = \beta = \gamma = 90^\circ$ |
| Tetragonal | $a = b \ne c$ | $\alpha = \beta = \gamma = 90^\circ$ |
| Orthorhombic | $a \ne b \ne c$ | $\alpha = \beta = \gamma = 90^\circ$ |
| Rhombohedral | $a = b = c$ | $\alpha = \beta = \gamma \ne 90^\circ$ |
| Hexagonal | $a = b \ne c$ | $\alpha = \beta = 90^\circ, \gamma = 120^\circ$ |
| Monoclinic | $a \ne b \ne c$ | $\alpha = \gamma = 90^\circ \ne \beta$ |
| Triclinic | $a \ne b \ne c$ | $\alpha \ne \beta \ne \gamma \ne 90^\circ$ |
Theoretical density
The theoretical density, $\rho$, of a crystal structure can be calculated as:
$$\rho = \frac{M}{N_A V}$$
Where $M$ is the total atomic weight of the atoms inside the unit cell in grams per mol, $N_A$ is Avogadro's constant of $6.022\times 10^{23} \text{mol}^{-1}$, and $V$ is the volume of the unit cell in $cm^3$.
Glossary
| Term | Meaning |
|---|---|
| Atomic mass unit | Mass of one proton or neutron, $\approx 1.66\times 10^{-24}\text{g}$ |
| Avogadro's number | $N_A$, number of protons/neutrons needed to produce a mass of $1\text{g}$, $\approx 6.022\times 10^{23}$ |
| Bond length | Separation between two bonded atoms |
| Electron | Elementary particle present with negative charge that orbits the nucleus with mass $\approx 9.11\times 10^{-26}$ |
| Mole | "Avogadro's number" of a molecule |
| Proton | Elementary particle present with positive charge that is fixed in the nucleus |
References
Li Yuning, ECE 109 Materials Chemistry for Engineers, Accessed 2024, [Slides]
James F. Shackelford, Introduction to Materials Science for Engineers, 8th ed, [Book]
Pavan M. V. Raja, Andrew R. Barron, An Introduction to X-ray Diffraction, Accessed 2024-02-13, [Online]